Project Euler にチャレンジ：Problem 68

次のMagic 3-gon ring について考えます、1-6 の数字を入れて、それぞれのラインの和が9になります。

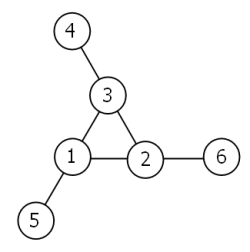
時計回りに、数値的に最も低い外部ノードを持つ3つのグループ（この例では4,3,2）から始めると、各解は一意に記述することができます。
例えば、上記の解は、以下の集合で記述することができます。4,3,2; 6,2,1; 5,1,3.
9,10,11,12 の 4種類の合計で環を完成させることが可能です。合計で8つの解が存在します。
解の合計セット
9 4,2,3; 5,3,1; 6,1,2
9 4,3,2; 6,2,1; 5,1,3
10 2,3,5; 4,5,1; 6,1,3
10 2,5,3; 6,3,1; 4,1,5
11 1,4,6; 3,6,2; 5,2,4
11 1,6,4; 5,4,2; 3,2,6
12 1,5,6; 2,6,4; 3,4,5
12 1,6,5; 3,5,4; 2,4,6

各グループを連結することで9桁の文字列を作ることができ、3-gon ringの最大文字列は432621513 になります。
1から10までの数字を用い、その配置によって16桁、17桁の文字列を構成することができます。Magic 5-gon ring の最大16桁の文字列はいくつか？